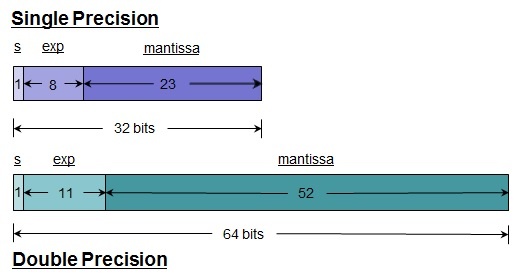
Java uses the IEEE 754 standard for floating-point representation. In this representation, floats are encoded using 1 sign bit, 8 exponent bits, and 23 mantissa bits. Doubles are encoded and used exactly the same way, except they use 1 sign bit, 11 exponent bits, and 52 mantissa bits. These bits encode the values of s, the sign; M, the significand; and E, the exponent. Floating-point numbers are then calculated as (-1)s * M * 2 E.
Ordinarily, all of the mantissa bits are used to express significant figures, in addition to a leading 1, which is implied and consequently omitted. As a result, floats have 24 significant bits of precision, and doubles have 53 significant bits of precision. Such numbers are called normalized numbers.
When the value to be represented is too small to encode normally, it is encoded in denormalized form, indicated by an exponent value of Float.MIN_EXPONENT - 1 or Double.MIN_EXPONENT - 1. Denormalized floating-point numbers have an assumed 0 in the ones' place and have one or more leading zeros in the represented portion of their mantissa. These leading zero bits no longer function as significant bits of precision; consequently, the total precision of denormalized floating-point numbers is less than that of normalized floating-point numbers. Note that even using normalized numbers where precision is required can pose a risk. See rule NUM04-J. Do not use floating-point numbers if precise computation is required for more information.
Using denormalized numbers can severely impair the precision of floating-point calculations; as a result, denormalized numbers must not be used.
Detecting Denormalized Numbers
The following code tests whether a float value is denormalized in FP-strict mode or for platforms that lack extended range support. Testing for denormalized numbers in the presence of extended range support is platform-dependent; see rule NUM53-J. Use the strictfp modifier for floating-point calculation consistency across platforms for additional information.
strictfp public static boolean isDenormalized(float val) {
if (val == 0) {
return false;
}
if ((val > -Float.MIN_NORMAL) && (val < Float.MIN_NORMAL)) {
return true;
}
return false;
}
Testing whether values of type double are denormalized is analogous.
Print Representation of Denormalized Numbers
Denormalized numbers can also be troublesome because their printed representation is unusual. Floats and normalized doubles, when formatted with the %a specifier, begin with a leading nonzero digit. Denormalized doubles can begin with a leading zero to the left of the decimal point in the mantissa.
Here is a small program, along with its output, that demonstrates the print representation of denormalized numbers.
strictfp class FloatingPointFormats {
public static void main(String[] args) {
float x = 0x1p-125f;
double y = 0x1p-1020;
System.out.format("normalized float with %%e : %e\n", x);
System.out.format("normalized float with %%a : %a\n", x);
x = 0x1p-140f;
System.out.format("denormalized float with %%e : %e\n", x);
System.out.format("denormalized float with %%a : %a\n", x);
System.out.format("normalized double with %%e : %e\n", y);
System.out.format("normalized double with %%a : %a\n", y);
y = 0x1p-1050;
System.out.format("denormalized double with %%e : %e\n", y);
System.out.format("denormalized double with %%a : %a\n", y);
}
}
normalized float with %e : 2.350989e-38 normalized float with %a : 0x1.0p-125 denormalized float with %e : 7.174648e-43 denormalized float with %a : 0x1.0p-140 normalized double with %e : 8.900295e-308 normalized double with %a : 0x1.0p-1020 denormalized double with %e : 8.289046e-317 denormalized double with %a : 0x0.0000001p-1022
Noncompliant Code Example
This noncompliant code example attempts to reduce a floating-point number to a denormalized value and then restore the value.
float x = 1/3.0f;
System.out.println("Original : " + x);
x = x * 7e-45f;
System.out.println("Denormalized: " + x);
x = x / 7e-45f;
System.out.println("Restored : " + x);
Because this operation is imprecise, this code produces the following output when run in FP-strict mode:
Original : 0.33333334 Denormalized: 2.8E-45 Restored : 0.4
Compliant Solution
Do not use code that could use denormalized numbers. When calculations using float produce denormalized numbers, use of double can provide sufficient precision.
double x = 1/3.0;
System.out.println("Original : " + x);
x = x * 7e-45;
System.out.println("Normalized: " + x);
x = x / 7e-45;
System.out.println("Restored : " + x);
This code produces the following output in FP-strict mode:
Original : 0.3333333333333333 Normalized: 2.333333333333333E-45 Restored : 0.3333333333333333
Exceptions
NUM54-J-EX0: Denormalized numbers are acceptable when suitable numerical analysis demonstrates that the computed values meet all accuracy and behavioral requirements appropriate to the application.
Risk Assessment
Floating-point numbers are an approximation; denormalized floating-point numbers are a less precise approximation. Use of denormalized numbers can cause unexpected loss of precision, possibly leading to incorrect or unexpected results. Although the severity for violations of this rule is low, applications that require accurate results should make every attempt to comply.
Rule | Severity | Likelihood | Detectable | Repairable | Priority | Level |
|---|---|---|---|---|---|---|
NUM54-J | Low | Probable | No | No | P2 | L3 |
Related Vulnerabilities
CVE-2010-4476 [CVE 2008 ] reports a vulnerability in the Double.parseDouble() method in Java 1.6 update 23 and earlier, Java 1.5 update 27 and earlier, and 1.4.2_29 and earlier. This vulnerability causes a denial of service when this method is passed a crafted string argument. The value 2.2250738585072012e-308 is close to the minimum normalized, positive, double-precision floating-point number; when encoded as a string it triggers an infinite loop of estimations during conversion to a normalized or denormalized double.
Related Guidelines
Bibliography
Computer Systems: A Programmer's Perspective, Section 2.4, Floating Point | |
[CVE 2008 ] | |
[IEEE 754] | |
| [Seacord 2015] | NUM05-J. Do not use denormalized numbers LiveLesson |